Théorie des supercordes La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Origine, raison, hasard Historiquement, la théorie des supercordes est née d’une théorie plus ancienne _la théorie des cordes_ qui avait été élaborée par Veneziano en 1968 pour tenter d’expliquer le confinement des quarks dans les hadrons. Veneziano avait introduit les cordes pour tenter d’expliquer pourquoi les quarks restaient confinés dans les baryons et les mésons. Les cordes jouaient le rôle de "ressorts" tendus entre les quarks, les maintenant ainsi dans un espace confiné. Avec la construction de la chromodynamique quantique (QCD), la théorie des cordes fut abandonnée, cependant certains résultats théoriques éveillèrent l’intérêt des physiciens. En effet, en 1969 Schwarz et Scherk montrèrent que les cordes fermées, c'est-à-dire en forme de boucles se comportaient comme des particules de masse nulle et de spin 2. Par conséquent, les cordes fermées n’étaient rien d’autre que des gravitons ! ! ! La théorie des cordes enfermait donc en elle-même la gravitation, sans devoir l’introduire de façon ad hoc (qui convient au sujet). La théorie des supercordes devaient également incorporer les dernières avancées théoriques sur le front des symétries. Ainsi, on imposa aux supercordes d’obéir à la supersymétrie, d’où le nom de supercordes.

Comprendre simplement  Up Page Le champ chromo-électrique Ici on étudie les cordes étendues entre les quarks comme les conséquences d'un espace ayant les propriétés d'un super-conducteur.   Ventres et nœuds La longueur de toutes ces cordes serait des milliards de milliards de fois inférieure à celle du diamètre d'un noyau d'atome. Et lors de diverses observations à des échelles plus importantes elles apparaîtraient comme ponctuelles et a ce moment là on retrouverait les particules que nous observons habituellement. L'échelle des longueurs de ces cordes approche 10-35m ,ce qui se rapproche très fortement de la longueur limite de Planck (longueur qui représenterait la plus petite dimension possible). Toujours dans cette voie on peut dire que plus le mode de vibration est compliqué ou complexe et plus la particule à laquelle cette vibration correspondrait serait massive.     Transformation de Lorentz La théorie des cordes n’était pas relativiste, c'est-à-dire que la description des cordes ne répondait pas aux exigences d’invariance par transformation de Lorentz (schématiquement, une transformation de Lorentz consiste en la contraction des distances et la dilatation des temps, conformément à des formules de transformation).   Comme les cordes d’un instrument de musique, les supercordes peuvent vibrer selon plusieurs modes. Le premier mode comprend un ventre et deux nœuds (les ventres sont les points où l’amplitude de l’oscillation est la plus forte, les nœuds sont les points où cette amplitude est nulle, comme c’est le cas aux extrémités de la corde vibrante). Le second mode comprend deux ventres et trois nœuds. Le troisième mode trois ventres et quatre nœuds et ainsi de suite. Chaque mode de vibration correspond à un type de particule.

Domaines de présence  Up Page Modélisation La modélisation théorique des supercordes laisse la liberté de choix de certains paramètres initiaux, que l’on appelle traditionnellement des conditions aux limites. Notamment, le mouvement des extrémités des supercordes n’est pas soumis à des contraintes rigides posées a priori mais peut être considéré comme un paramètre libre de la théorie. On distingue ainsi deux types d’extrémités pour les supercordes ouvertes : _Celles qui peuvent se déplacer mais en étant entraînées uniquement par le mouvement de la supercorde. Elles obéissent à la condition aux limites de Neuman. _Celles qui restent fixes dans un hyperplan. Elles répondent à la condition aux limites de Dirichlet. 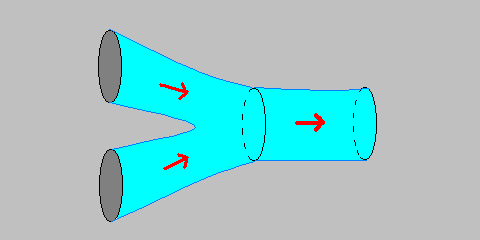  L’interaction entre deux supercordes prend une signification physique très simple. Lorsque deux supercordes interagissent, elles se fondent l’une à l’autre. Elles peuvent par la suite se scinder de nouveau en une ou plusieurs supercordes. Dans tous les cas, les processus mis en jeu sont intuitivement simples.   Très schématiquement, les supercordes présentent deux intérêts majeurs : _Les cordes fermées possèdent les mêmes propriétés que les gravitons et peuvent donc être assimilées comme tels _Les cordes sont des entités physiques ayant une dimension non nulle, alors que les particules, selon l’acceptation courante, sont ponctuelles et sans dimension.   La première propriété permet à la théorie des supercordes d’inclure naturellement la gravitation. La seconde propriété permet de s’affranchir de toutes les difficultés inhérentes à la nature ponctuelle des particules, notamment les divergences dans le calcul des probabilités de diffusion (divergences de la matrice S). Le développement perturbatif d’une interaction selon la théorie des supercordes donne un résultat fini qui est illustré dans la figure suivante.

Son interprétation dans l'avenir  Up Page Monde futur

Les références  Up Page Réseau Pepe Automates Intelligents   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Ce que vous avez toujours voulu savoir "La théorie des supercordes est la seule aujourd'hui qui unifie la physique quantique et la relativité générale, en ceci elle est admirable. Certains estiment de surcroît qu'elle aurait des conséquences vérifiables par l'expérimentation, comme la possibilité de créer des mini-trous noirs dans des collisions violentes de particules. Ces minuscules trous noirs se désintégreraient aussitôt sans créer le moindre risque." Michel Cassé, astrophysicien, directeur de recherche au Commissariat è l'Energie Atomique (CEA).