Accueil Arborescence Page précédente
|
Nième dimension
La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore … |
|
by Pepe © Accueil Arborescence Page précédente |

|
|
La petite histoire Up Page Dimensions supplémentaires Les physiciens en sont aujourd'hui convaincus: il doit exister d'autres dimensions que celles d'espace et de temps dans lesquelles nous évoluons. Des dimensions si petites que nous ne les percevons même pas, ou tellement grandes que nous n'y avons pas accès, mais qui permettent de rendre l'Univers enfin cohérent avec la théorie. |
|
Comprendre simplement Up Page 1907 Grâce aux travaux du mathématicien russe Hermann Minkowski et du physicien allemand Albert Einstein, aux trois dimensions d'espaces que nous connaissons, il faut en ajouter une quatrième, qui leur est intimement liée. Une dimension un peu différente des autres: le temps (concept espace-temps). Dans cette dimension-là, vous êtes forcé de vous déplacer toujours dans le même sens, du passé vers l'avenir. Une particularité que les physiciens, aujourd'hui encore, ne parviennent par vraiment à expliquer. 1919 Mathématicien polonais, Theodor Kaluka s'aperçoit qu'en ajoutant une dimension supplémentaire dans les équations de la toute jeune relativité générale d'Einstein (1916), la nouvelle théorie de la gravitation, on retombe sur les équations de Maxwell décrivant l'électromagnétisme. Les équations de Maxwell seraient donc cachées dans celles d'Einstein, pour autant que nous vivons dans un monde à cinq dimensions! Le mathématicien suédois Oskar Klein propose une explication en 1926: c'est parce qu'elle est beaucoup plus petite. Si petite qu'aucun instrument de mesure ne pourra même jamais déceler son existence. 1980 Selon la théorie des cordes, les particules et les forces ne seraient que les manifestations du frémissement de minuscules cordes, qui doivent impérativement vibrer dans dix, voir onze dimensions. 10 dimensions  Les physiciens qui sont adeptes de cette théorie des
supercordes pensent aussi que la matière est
constituée de ces cordes et que ces cordes
possèdent 10 dimensions. Nous en connaissons 4 (longueur,
largeur, profondeur et temps) , les 6 seraient en fait
située proche d'une échelle proche de 10-35 m et
elles seraient enroulées sur elles même (au
delà de cette limite qui est la longueur de Planck il semble
en effet que notre physique soit complètement impuissante
pour décrire le monde tel qu'il pourrait être). De
plus lorsque plusieurs cordes se rencontreraient elle se regrouperaient
pour ne former plus qu'une seule et à ce moment
là elles pourraient à volonté
à nouveau se scinder en plusieurs cordes qui n'auraient pas
forcément la même forme de vibration (ce qui
pouvait être le cas des cordes que nous venons
d'évoquer précédemment). Il y en a en
fait 5 distinctes et qui s'opposent plus ou moins. Pour certains, ces 5
théories sont en fait plusieurs variantes d'une seule et
même théorie dite théorie M car
théorie qui décrirait l'action de petite corde
sur des membranes... On peut donc voir que même la
théorie du Tout est encore a unifier!
Les physiciens qui sont adeptes de cette théorie des
supercordes pensent aussi que la matière est
constituée de ces cordes et que ces cordes
possèdent 10 dimensions. Nous en connaissons 4 (longueur,
largeur, profondeur et temps) , les 6 seraient en fait
située proche d'une échelle proche de 10-35 m et
elles seraient enroulées sur elles même (au
delà de cette limite qui est la longueur de Planck il semble
en effet que notre physique soit complètement impuissante
pour décrire le monde tel qu'il pourrait être). De
plus lorsque plusieurs cordes se rencontreraient elle se regrouperaient
pour ne former plus qu'une seule et à ce moment
là elles pourraient à volonté
à nouveau se scinder en plusieurs cordes qui n'auraient pas
forcément la même forme de vibration (ce qui
pouvait être le cas des cordes que nous venons
d'évoquer précédemment). Il y en a en
fait 5 distinctes et qui s'opposent plus ou moins. Pour certains, ces 5
théories sont en fait plusieurs variantes d'une seule et
même théorie dite théorie M car
théorie qui décrirait l'action de petite corde
sur des membranes... On peut donc voir que même la
théorie du Tout est encore a unifier!
|
|
Domaines de présence Up Page Des dimensions cachées Pour matérialiser mentalement les trois dimensions (longueur, largeur, hauteur), il suffit d'imaginer trois axes immenses perpendiculaires les uns aux autres. Prétendre que l'Univers est plat (espace euclidien), signifie que ces trois axes se prolongeraient indéfiniment: nous serons donc là en présence d'un espace infini. Rien n'interdit que l'Univers soit un espace fini (espace non euclidien). Dans ce cas, à la manière d'une sphère, les axes finiraient par faire une boucle sur eux-mêmes. Lorsque les scientifiques parlent d'une petite dimension supplémentaire, il s'agit évidemment d'une dimension finie. C'est donc une petite boucle d'espace: si on la parcourt, on finit toujours par revenir au même endroit. Quant à la taille de ces hypothétiques dimensions _autrement dit la diamètre de ces boucles_ pour des raisons de cohérence théorique, les physiciens l'estiment à 10-35m .Ce qui correspond à la longueur de Planck. Dans les années 90, le physicien Ignatios Antoniadis, qui travaille à l'école polytechnique, s'aperçoit que le diamètre des dimensions supplémentaires peut atteindre 10-18m, sans que cela contredise les impératifs de la théorie des cordes. 
 Pour un équilibriste, un fil ressemble à un espace à une
dimension: elle ne peut qu'avancer ou reculer. Une fourmi, en revanche, perçoit
une petite dimension supplémentaire, enroulée sur elle-même:
le diamètre du fil. Elle peut ainsi en faire le tour. Un espace à trois dimensions, comme une sphère, peut révéler,
à très petite échelle, des petites dimensions supplémentaires
entortillées.
Pour un équilibriste, un fil ressemble à un espace à une
dimension: elle ne peut qu'avancer ou reculer. Une fourmi, en revanche, perçoit
une petite dimension supplémentaire, enroulée sur elle-même:
le diamètre du fil. Elle peut ainsi en faire le tour. Un espace à trois dimensions, comme une sphère, peut révéler,
à très petite échelle, des petites dimensions supplémentaires
entortillées.
|
|
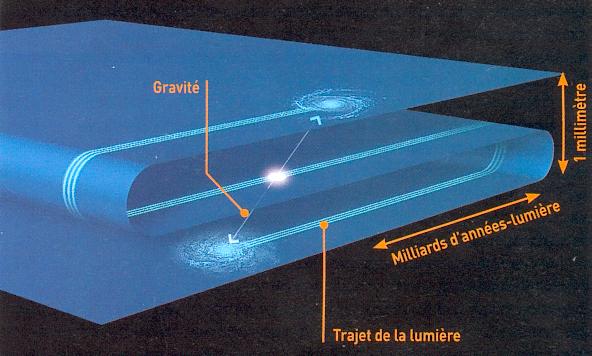
Son interprétation dans l'avenir Up Page Un monde de branes  Les dimensions supplémentaires permettraient d'expliquer pourquoi la force de gravitation (qui règne entre ces corps massifs, comme les planètes et les étoiles) est si faible par rapport aux trois autres forces de la nature (la force électromagnétique, la force nucléaire forte et la force nucléaire faible). Pour se les représenter, il faut aplatir mentalement notre espace à trois dimensions en un plan à deux dimensions. Cette membrane d'espace est ce que les physiciens appellent notre "brane" (l'espè de voile que vous voyez ci-contre). Les dimensions supplémentaires sont représentées par le pavé quadrillé. 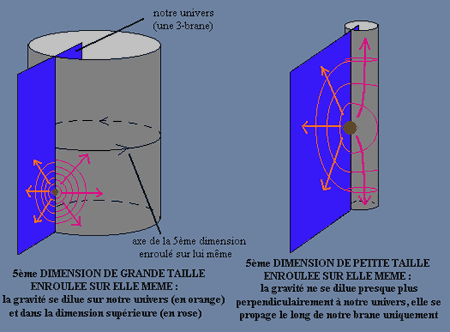 En dehors, il existerait des dimensions supplémentaires cycliques, représentées ici comme un cylindre quadrillé. Toute la matière (les galaxies), ainsi que les forces électromagnétique et nucléaires resteraient enfermées dans cette brane. Seule la gravitation (représentée en rouge) pourrait se propager à la fois dans la brane et dans les autres dimensions. Ainsi, elle se diluerait dans cette espace supplémentaire, et nous la percevrions comme atténuée, alors qu'en réalité, elle serait aussi intense que les autres forces.  Selon les calculs des physiciens,
dans le cas où il existerait deux dimensions supplémentaires, leur
diamètre avoisinerait le millimètre…
Cette théorie, de la dissipation de la gravitation dans des dimensions
supplémentaires, a été proposée par trois physiciens,
Nima Arkani-Hamed, Savas Dimopoulos et Gia Dvali, tous trois de l'université
de Stanford, en Californie, en 1998.
Selon les calculs des physiciens,
dans le cas où il existerait deux dimensions supplémentaires, leur
diamètre avoisinerait le millimètre…
Cette théorie, de la dissipation de la gravitation dans des dimensions
supplémentaires, a été proposée par trois physiciens,
Nima Arkani-Hamed, Savas Dimopoulos et Gia Dvali, tous trois de l'université
de Stanford, en Californie, en 1998.
|
|
Les références Up Page Réseau Pepe Science et Vie Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). |
|
Mais encore … Up Page Matière sombre  Un an plus tard, en 1999, Lisa Randall, alors chercheuse à l'université de Princeton (New Jersey, Etats-Unis) et au MIT (Massachusetts Institute of Technology), et Raman Sundrum, de l'université de Boston (Massachusetts) suggèrent que l'une des dimensions supplémentaires pourrait être infinie! A condition, toutefois, que la gravitation n'aille se perdre totalement dans cette dimension, mais reste principalement concentrée aux alentours de notre brane. Cette fois, il ne s'agit plus d'une petite boucle, mais d'une dimension qui ressemblerait beaucoup à celles que nous connaissons. "Notre grand univers, celui que nous voyons, n'est peut-être qu'un petit détail dans un espace bien plus grand encore!", commente avec enthousiasme Nima Arkani-Hamed. L'espace des physiciens est bel et bien en train de s'élargir. Sans pour autant que cela remette en question leur interprétation du monde qui nous entoure. "Les dimensions supplémentaires ne modifient pas les lois de la physique, mais elles constituent une nouvelle arène pour les utiliser. Et cela est fascinant", confie Lisa Randall. Les scientifiques savent aujourd'hui que plus de 90% de la masse de l'Univers
échappe à leurs observations. Ils constatent les effets gravitationnels
de cette matière sombre sur l'espace environnant, mais ne parviennent
pas à la voir.
|