La marche des tortues La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Les commandes de la tortue Przemsylaw Prusinkiewic, de l'Université de Calgary, a developpé des techniques utilisant les symboles interprétés comme des <"commandes tortue". De quoi s'agit-il ? Dans les années 1960, Seymour Papert a conçu un langage informatique pour développer l'imagination des enfants et dont l'idée est la suivante: une tortue dessine une image en laissant traîner sa queue qu'elle soulève pour créer un dessin discontinu. La tortue n'a pas de vision globale, mais elle crée des dessins complexes en comprenant et en exécutant un ensemble limité d'instructions simples qui lui sont transmises par un ensemble de symboles. Ainsi, "F" signifie "avancer d'un pas en traçant un trait"; "f", "avancer d'un pas en soulevant la queue"; "+", "tourner à gauche (dans le sens inverse des aiguilles d'une montre) d'un angle de d degrés"; "?", "tourner à droite (dans le sens des aiguilles d'une montre) d'un angle de d degrés".

Comprendre simplement  Up Page L-Langage Pour chaque dessin, il faut d'abord spécifier la direction de la tortue et l'angle d, qui reste le même pendant tout le tracé. Chaque déplacement commence à l'endroit où s'est terminé le précédent. Une technique mathématique d'ajustement de données, permettrait de créer une courbe arrondie sans points anguleux. Si nous réduisons la taille des pas de la tortue pour chaque résultat de sorte que les dessins successifs tiennent dans un carré de la même taille (on parle de renormalisation), et si nous continuions sans fin, nous aurions un résultant surprenant: une variante de la courbe fractale connue sous le nom de courbe de Sierpinski, du nom du mathématicien qui la décrivit en 1912.

Domaines de présence  Up Page Familles de kolam Les familles de kolam réunissent les figures qui partagent des caractéristiques communes, ou sont dérivées les unes des autres.   Liane de Parijatha (arbre sacré) Ces trois figures de kolams appartiennent à la famille de la Liane de Parijatha (un arbre sacré). 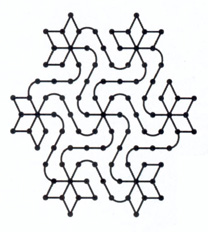  Serpents Les serpents  sont des figures de kolam que l'on peut produire grâce à un langage graphique. La plus petite des figures (a) est constituée d'une chaîne de départ B--F--B--F, où "F" signifie avaner d'un pas, "-" signifie se déplacer de 45 degrés dqns le sens des aiguilles d'une montre, "+" signifie se déplacer de 45 degrés dans ke sens inverse des aiguilles d'une montre, et "B" signifie F +F +F --F --F +F +F. En appliquant la règle de réécriture B = B +F +B --F --B +F +B, on produit des versions plus complexes de la figure du Serpent. Le premier résultat (b), la chaîne de départ B--F--B--F devient (B +F +B --F --B +F +B)--F--(B +F +B --F --B +F +B)--F. Chaque application de la règle de réécriture remplace chaque bras de la croix à quatre bras par une nouvelle croix à quatre bras, ce qui entraîne une croissance exponentielle du nombre de bras: quatre bras (a), puis 16 (b), puis 64 (c) et ainsi de suite. 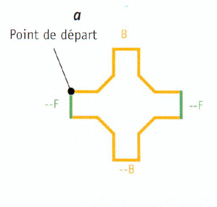 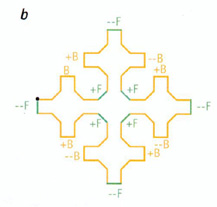 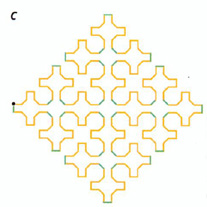  Bracelets de Krishna Les bracelets de Krishna sont une famille de figures de kolam que l'on peut fabriquer avec un langage graphique. On utilise la chaîne de départ R1FR2FR2FR2FR1 [(a), chaque lettre désigne un élément, par exemple F représente un segment vert] et les règles (dans l'encadré) qui dictent le devenir de chaque symbole de la chaîne pour créer des formes de plus en plus complexes. Chaque application des règles de réécriture (b et c) remplace chacune des "feuilles" par un ensemble de quatre "feuilles". 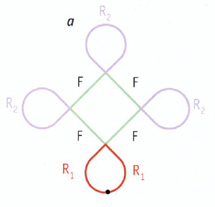 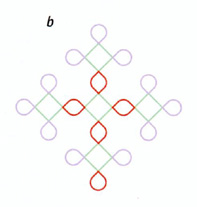 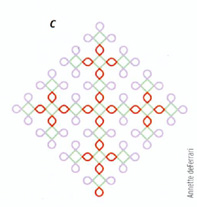  Règles F: avancer en tirant un trait R1: avancer en faisant un demi-tour vers la droite R2: avancer en faisant une boucle complète vers la droite. Règles de réécriture F: F R1: R1FR2FR1 R2: R1FR2FR2FR2FR1

Son interprétation dans l'avenir  Up Page Monde futur

Les références  Up Page Réseau Pepe Pour la Science avril / juin 2005 Mathématiques exotiques n°47   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Ce que vous avez toujours voulu savoir