Accueil Arborescence Page précédente
© Houdini
|
L-Systèmes ou Fractales La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore … |
|
by pepe © Accueil Arborescence Page précédente |
|
© Houdini |
|
La petite histoire Up Page Origine, raisons, hasard Nous sommes tous habitués aux objets de la géométrie euclidienne: aux droites, aux cercles, aux rectangles, aux cubes... Ils nous permettent de décrire simplement ce que l'on trouve dans la nature. Ainsi, les troncs d'arbres sont approximativement des cylindres et les oranges des sphères. Mais comment fait-on pour décrire un chou-fleur, un flocon de neige, les poumons, les fluctuations des marchés boursiers ou même un arbre entier? En effet, les choses se compliquent, la géométrie euclidienne a atteint sa limite. Les scientifiques ne se sont pas découragés, et les mathématiciens ont montré l'intérêt de la géométrie fractale pour caractériser les objets "ayant la propriété de pouvoir être décomposés en parties de telle façon que chaque partie soit une image réduite du tout". Vous l'avez bien compris, la géométrie fractale permet de caractériser des objets ayant une forme très irrégulière, et qui ont la propriété d'invariance par changement d'échelle. C'est à dire que si vous regardez un objet fractal au microscope ou à l'oeil nu, vous allez voir la même chose. Cette particularité d'auto-similarité est très étonnante, et les fractales ont bien d'autres propriétés, plus fascinantes les unes que les autre. Découvreurs Les premiers fractales n'étaient pas vraiment des fractales, elles étaient plutôt des expérimentations mathématiques. Ces objets constituaient pour les mathématiciens des erreurs ou des exceptions de la géométrie. Nous avons retracé ces formes à partir du XV siècle par Albrecht Dürer et un pentagone spécial. En 1905 Jean Perrin remarque en observant un colloïde (système de particules en suspension dans un fluide) obtenu en salant de l'eau de savon comme sa forme révèle de nouvelles irrégularités chaque fois qu'on l'observe avec un meilleur grossissement "sans jamais éprouver l'impression nette et reposante que donne, par exemple, une bille d'acier poli..." Le nom "L-système" vient du nom du biologiste Aristid Lindenmayer qui les inventa, en 1968, pour formaliser la croissance des plantes. Les L-systèmes nous sont surtout connus dans les mathématiques par le biais des fractales. Le mot "fractal" (du latin fractus, 'brisé') est un mot inventé par le mathématicien français Benoît Mandelbrot en 1975, qui signifie "uniformément fragmenté ou irrégulier et auto-similaire ou structurellement invariant selon l'échelle". Elles sont à la base d'un nouveau système de géométrie permettant de représenter des objets très irréguliers tels que les reliefs montagneux, les amas galactiques ou les côtes rocheuses très découpées (géométrie fractale). Apparues au XIXe siècle, les fractales sont considérées comme des curiosités mathématiques jusqu'au milieu du XXe siècle. Elles n'acquièrent un statut à part entière que dans les années soixante-dix, grâce au mathématicien français Benoît Mandelbrot qui en fait l'objet d'une nouvelle discipline mathématique: la géométrie fractale. En géométrie euclidienne, les figures ont une dimension entière: 0 pour un point, 1 pour une courbe, 2 pour une surface et 3 pour un volume. En revanche, la dimension d'une fractale peut prendre des valeurs qui ne sont pas des nombres entiers: la dimension fractale constitue une généralisation de la notion de dimension utilisée en géométrie euclidienne. |
||||||||||||||||||||||||||||||
|
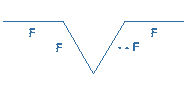
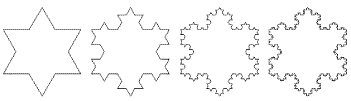
Comprendre simplement Up Page Définition Un L-Système est un groupe de règles et de symboles qui modélise un processus de croissance. Ces règles permettent de construire une chaine de symboles qui sera modifié à chacune des étapes de la modélisation. Prenons un exemple. Au départ nous avons un élément: A. Nous établissons une règle qui dit que à chaque fois que l'on voit un A, on le transforme en B, et à chaque fois que l'on voit un B, on le transforme en AB. Soit les règles suivantes: A –> B et B –> AB. Nous obtenons donc à la première génération: B. Et à la deuxième génération: AB. Et ainsi de suite. 3e génération: BAB. 4e génération: ABBAB. 5e génération: BABABBAB. 6e génération: ABBABBABABBAB. Etc. Exemple de L-Système Maintenant que l'on a une suite de symboles, qu'en faire? Leur donner un sens! Imaginez que vous êtes une tortue évoluant dans un plan. On vous donne un chemin précis à parcourir à l'aide d'ordres répétitifs. Si l'on vous dit, pour "F" vous avancez d'un pas devant vous, et pour "+" ou "-" vous tournez respectivement à droite ou à gauche de 60°. A l'aide des L-Systèmes, vous parcourerez ainsi à chaque génération le même chemin mais vous le répéterez de plus en plus souvent. Commencons par l'ordre: F--F--F. Appliquons la règle: F –> F+F--F+F. Nous obtenons à la première itération: F+F--F+F--F+F--F+F--F+F--F+F. Cet exemple génère en fait le flocon de Von KOCH.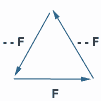 
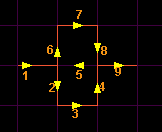
Les commandes de la tortue F : avancer dans la direction courante en dessinant. f : avancer dans la direction courante sans dessiner. + : tourner à droite d'un angle 360/nombre de directions. - : idem pour tourner à gauche. c : passer à la couleur suivante. | : faire demi-tour (tourner de 180°) [ : création d'un n&eolig;ud. ] : retour au nœud précédent de niveau correspondant. Les symboles ' @ ' et ' ! ' sont également utiles, ils permettent respectivement d'agrandir ou de réduire tel ou tel motif et d'interchanger le sens de dessin. |
||||||||||||||||||||||||||||||
|
Domaines de présence Up Page Dimension 1 Branching patterns of herbaceous plants Un pattern, par opposition à la matière, différencie la forme (pattern, ordre, qualité) à la substance (matière, structure, quantité). Subapical growth  
L'allongement d'une tige est la manifestation directement observable de la croissance
primaire.
Il est essentiellement le résultat d'un allongement cellulaire qui prend naissance un peu en arrière du dôme apical, d'où le qualificatif de "subapical growth" employé par Hackett (1985). Ce phénomène, qui concerne essentiellement l'étirement des entre-noeuds, est encore appelé "croissance internodale". Tout ce qui se trouve "entre crochets", sera situé sur la même branche ! 
Herbe 2
Premise (axiome, départ): F Alpha (angle) = pi/8 (ou 22,5 degrés) Rule 1: F = F[+F]F[-F]F 
Herbe
Premise (axiome, départ): X Alpha (angle) = pi/8 (22,5 degrés) Rule 1: X = F [- X] F [- X] + X Rule 2: F = F F 
Broussaille
Premise (axiome, départ): F Alpha (angle) = pi/8 (ou 22,5 degrés) Rule 1 (Génération 1): F = FF-[-F+F+F]+[+F-F-F] 
Fougère courbe
Premise (axiome, départ): A Alpha (angle) = pi/4 (ou 45 degrés) Constante b = 4 Rule 1 (Génération 1): A = F +[+FA] F [-FA] +(b)A 
Fougère droite
Premise (axiome, départ): X Alpha (angle) = pi/4 (ou 45 degrés) Rule 1 (Génération 1): X = F [-X] F [+X] F Monopodial branching (raceme) 
Ses branches latérales portent des
bourgeons (cercle rose)
et puis des fleurs (rond rose), mais ne
s'embranchent (se ramifient) pas pour promouvoir. La structure résultante s'appelle une
structure monopodiale (flêche verte),
et l'inflorescence correspondante s'appelle un raceme (grappe).
La Capsella Brousse-pastoris, ou la bourse du berger, suit ce principe, tout comme la Campanula rapunculoïdes (ici bas).  
Sympodial branching (cyme) 
Une structure sympodiale, produit un bourgeon
de fleur terminant le développement de l'axe courant (rond rose), mais produit
une ou plusieurs ramifications latérales actives. Ce processus se répète
périodiquement, avec la poussée principale
entrant toujours dans les branches latérales.
Le type résultant d'inflorescence s'appelle un cyme. Le développement du Coronaria de Lychnis (la lychnide rose) et la Centratenia grandifolia Melastomataceae, fournissent un bon exemple du processus décrit. 
Polypodial branching (panicle) 
La structure principale et les ramifications latéraux produisent
de nouvelles branches jusque à une certaine itération
(développement, sous-branche),
les ramifications subissent un changement de développemental
et sont transformées en bourgeons de fleur.
L'inflorescence résultante, appelée panicle, peut adopter de diverses formes selon les paramètres géométriques. 
La forme et la flore Une inflorescence résulte de la croissance d'un méristème (tissu embryonnaire situé à l'extrémité de la tige) qui donne périodiquement naissance soit à une fleur, soit à un nouveau méristème (et donc à une ramification). Aussi, au fil du temps, le nombre théorique de structures possibles augmente rapidement. Pourtant, seules quelques-unes sont connues, et on peut les regrouper en trois familles: les cymes, les grappes et les panicules. Toutes les inflorescences sont des variations autour de ces trois thèmes. Les biologistes et informaticiens ont défini, pour chaque méristème, un paramètre, noté veg, qui détermine le devenir de ce tissu: il donne une nouvelle tige pour des valeurs supérieures à un seuil, sinon une fleur. Des simulations ont permis d'explorer différents cas. Par exemple, lorsque veg diminue de la même façon dans chaque méristème, une panicule apparaît. En modifiant l'évolution de veg selon les méristèmes et en compliquant peu peu le modèle (en jouant sur l'évolution de vzg avec le temps), on obtient tous les types d'inflorescences. Ce modèle a également mis en évidence le rôle important du climat dans l'évolution des inflorescences: un climat tropical favoriserait les panicules, alors que les cymes et les grappes seraient plus probables sous des latitudes tempérées.  
 
 
Dimension 2 Triangle de Sierpinsky 
Premise (axiome, départ): X Alpha (angle) = pi/4 (ou 45 degrés) Rule 1 (Génération 1): X = F [-X] F [+X] 
Carré de Sierpinsky
Premise (axiome, départ): F Alpha (angle) = pi/2 (ou 90 degrés) Cote = cote/3 Rule 1 (Génération 1): F= F-F+F+F+f-F-F-F+F Rule 2 (Génération 2): f= f-f+f+f+f-f-f-f+f 
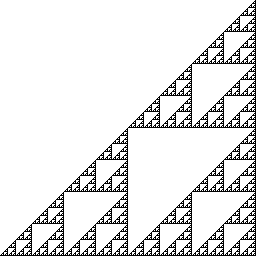Pour ce qui est des atuces de constructions, une des plus faciles à implémenter
est la méthode de substitution par matrices.
Par exemple avec une matrice 2x2 de ce type: ( 0 1 ) ( 1 1 ) Pour chaque 1 rencontré on remplace le coefficient par cette matrice, et pour chaque 0 on le remplace par une matrice nulle. Au bout d'un certain nombre de substititions (profondeur de récursion), on obtient une matrice NxN, où N est un nombre en puissance de 2 (l'exposant étant précisément la profondeur de récursion globale). Ansi 3 étapes nous donneront dans cette exemple une matrice 8x8. Au final, on obtiendra le triangle de Sierpinski ... Dimension 3 
|
||||||||||||||||||||||||||||||
|
Son interprétation dans l'avenir Up Page
Une fonction f(z), où z est un nombre complexe, est itéré un grand nombre de fois. Dans les réels, un nombre élevé au carré de façon répétée diverge vers l'infini aussitôt qu'il est plus grand que 1 ou plus petit que -1. Dans le cas contraire, la mise au carré le fait tendre vers 0. Le calcul dans les nombres complexes n'obéit plus à cette loi, la mise au carré impliquant deux composantes, le nombre réel et imaginaire. On dit alors qu'un point atteindra l'infini si sa distance à l'origine dépasse une valeur, comme 2. L'ensemble de Mandelbrot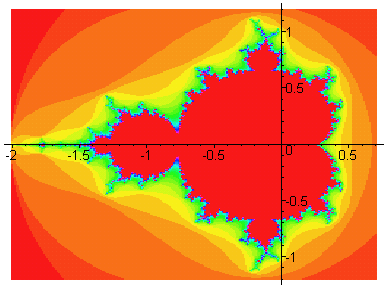 
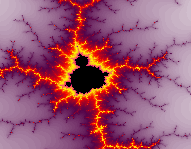 L'ensemble de Mandelbrot
consiste à decrire tous les points d'un plan complexe
dont une transformation les fait se contenir
dans un cercle de rayon 2. zn+1 = zn2 + c.
Les znet c sont des nombre complexes. Il existe quantité de fonctions qui donnent de magnifiques figures par itérations: z3, ez , etc... Le choix des couleurs étant arbitraire, on colorie généralement en noir les points qui font partie de l'ensemble et en blanc (ou souvent en dégradé de couleurs), tous les autres points. Pour les points à l'extérieur de l'ensemble, on attribue souvent une couleur selon le nombre d'itération nécessaire pour que zn atteigne l'infini. Ce nombre donne une idée de la vitesse à laquelle le point diverge. L'ensemble de Julia  Ces ensembles ont été
découverts par Gaston Julia à
une époque où il était difficile d'avoir un rendu graphique
sans l'aide de l'ordinateur. Il existe néanmoins une infinité d'ensembles de Julia dont chacun
n'est en réalité qu'une une représentation isolée
de l'ensemble de Mandelbrot en un point.
Ainsi, un ensemble de Julia est identifié par ses coordonnées dans le plan complexe. L'algorithme de calcul est donc très proche de celui de Mandelbrot. Pour obtenir des résultats intéressants, c doit se situer à l'intérieur de l'ensemble de Mandelbrot, le plus proche possible de la frontière entre l'intérieur et l'extérieur. Par exemple, voici quelques une des fractales possibles de Julia: c=0.3+0.6i, c=-0.0519+0.688i, c=0.32+0.43i, c=-0.0986-0.65186i. N'hésitez pas à vos servir du dessin de Mandelbrot, ci-dessus, muni d'un repère !! Quelques exemples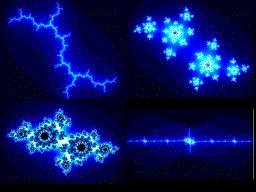 
Sur l'image ci-contre, voici respectivement les cinq
valeurs qui ont été choisies: c=0+i, c=-0,4+0,7i, c=-0,7+0,3i, c=-1,77+0,01i et c=-0,15+0,45i. 
Quelques propriétés utiles L' ensemble de Julia Jc est inclus dans le cercle de centre 0 et de rayon |c|+1. Tous les ensembles de Julia sont symétriques par rapport à 0. z0 et -z0 ont la même couleur. Si c est réel, Jc est symétrique par rapport &agr&ave; l'axe réel Si exist p : |zp| > max(2,|c|) alors la suite zn diverge. L'ensemble de Newton  La méthode de Newton est
très efficace pour estimer les zéros d'une fonction.
Contrairement à l'ensemble de Mandelbrot dans lequel l'infini agit comme
un attracteur sur chaque point du plan, la fractale de Newton attire ces derniers
vers des valeurs finies, réelles ou complexes, constituant les racines
_les valeurs x0 qui annule la fonction f(x), c'est-à-dire
f(x0)=0 _ d'un polynôme. Un polynôme est une fonction
du style axn+bxn+1...
On sait que la racine (x0), tel que f(x0)=0, d'une fonction compte autant de solutions, disposées autour d'un cercle, que le degré (exposant de x) de cette fonction. 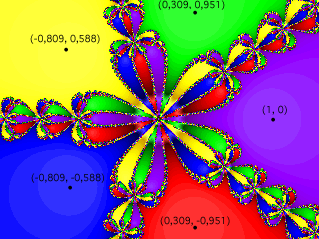 Prenons
f(x) = x5 - 1. La fonction possède 5 zéros sur l'ensemble
des nombres complexes: -0,809 + 0,588i ; 0,309 + 0,951i ; 1 ; 0,309 - 0,951i ;
-0,809 - 0,588i. Si on appliquait la méthode de Newton à f(x) en
utilisant une quelconque valeur pour x0, elle convergerait fort probablement vers
l'un ou l'autre des 5 zéros de la fonction. Lorsqu'on utilise une valeur
initiale suffisamment près d'un zéro, la méthode de Newton
converge en général très rapidement vers ce zéro.
Dans le cas contraire, elle peut tout aussi bien converger vers un autre zéro,
pas nécessairement celui qui est le plus près de x0.
 Si on considère
la fonction f(x) = x5 - 1, mais que cette fois-ci on
prenne comme valeurs de xo des nombres complexes dont les parties réelle
et imaginaire sont entre -1.5 et 1.5, on obtient ci-contre.
|
||||||||||||||||||||||||||||||
|
Les références Up Page Réseau Pepe Essai sur les fractales Architecture végétale Pour la Science août 2007 n°358 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). |
||||||||||||||||||||||||||||||
|
Mais encore … Up Page Paysage fractale Les matrices Méthode de Cramer Mathématiquement, on définit les transformations par une équation paramétrique donnant les valeurs des coordonnées en fonction des coordonnéees initiales. Ces équations ressemblent à celles-ci: x'=a.x+b.y+c.z+j y'=d.x+e.y+f.z+k z'=g.x+h.y+i.z+l On peut aussi écrire ces équations sous la forme d'une matrice.
La quatrième colonne n'effectue aucune transformation, elle ne permet que l'obtention d'une matrice carrée qui pourra éventuellement être inversée. Les coefficients de cette colonne ne doivent pas être modifiés pour conserver la logique de l'équation. Cette matrice permet de créer des fractales dans un espace à trois dimensions et les transformations effectuées s'avèrent un peu plus complexes. Par exemple, la rotation peut avoir lieu sur un nombre d'axe, non pas seulement sur un seul comme dans le plan. Pour obtenir des fractales en deux dimensions, on ignore simplement la ligne 3 et la colonne 3 de la matrice. La forme simpifiée pour la deuxième dimension s'écrit comme suit:
Fractales de Markus-Lyapounov Menu Editor 
|