Accueil Arborescence Page précédente


|
by Pepe © Accueil Arborescence Page précédente |


|
|
Fonctions polynômes Up Page De degré 1 (ou fonctions linéaires) Elles sont du type: f(x)=ax+b, où a et b sont des constantes et x étant la variable. Une autre écriture consiste à utiliser ce type de formule: ax+by+c=0, où (a,b,c) sont des constantes, x (abscisse) la variable et y (ordonnée) la fonction f(x).
De degré 2 (ou fonctions paraboliques) Elles sont du type: f(x)=ax2+bx+c, où a, b et c sont des constantes et x étant la variable. Les graphes sont des paraboles d'axe de symétrie verticale. L'axe de symétrie correspond à la valeur de x où la tangente est horizontale , c'est-à-dire pour laquelle: x=-b/2a. Discriminant: D =b2-4ac Le signe de a et celui de D (delta) permettent de placer la parabole par rapport aux axes
De degré 3 (ou fonctions cubiques) Elles sont du type: f(x)=ax3+bx2+cx+d, où a, b, c et d sont des constantes et x étant la variable. Influence du signe du discriminant D =4b2-12ca Notons de plus que f(x), polynôme de degré 3 a trois racines réelles (éventuellement confondues) ou une racine réelle et deux racines complexes conjuguées.
De degré 4 (ou fonctions quadratiques) Elles sont du type: f(x)=ax4+bx3+cx2+dx+e, où a, b, c, d et e sont des constantes et x étant la variable. Dans une autre écriture: f(x)=(x-a)(x-b)(x-c)(x-d), toutefois ici il ne s'agit pas des mêmes constantes (a,b,c,d) !

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonctions logarithme et exponentielle Up Page Fonctions exponentielles Les fonctions exponentielles sont du style: ax, où a est une constante. Il existe, aussi également, deux catégories de fonctions, celles dont la valeur 1<a<e (la fameuse constante d'Euler, équivalente à 2,718...), et celles dont a>e.
Fonctions logarithmes Les fonctions logarithmes sont du style: loga(x)=ln(x)/ln(a). Il existe deux catégories de fonctions, celles dont la valeur 1<a<e (la fameuse constante d'Euler, équivalente à 2,718...), et celles dont a>e. La fonction "ln(x)" se nomme "logarithme népérien". Lorsque a=10, la fonction sera appelée "logarithme décimal".

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonctions trigonométriques Up Page
Fonctionc trigonométriques inverses Arcsinus [arcsin(x) ou asin(x)] 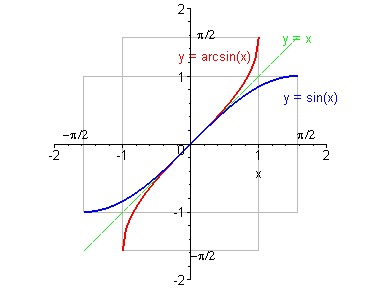
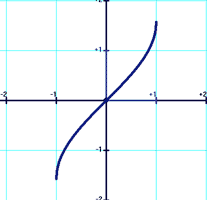
Arcosinus [arcos(x) ou acos(x)] 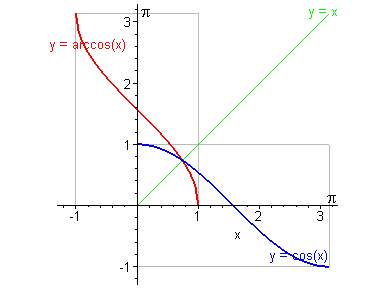

Arctangente [artan(x) ou atan(x)] 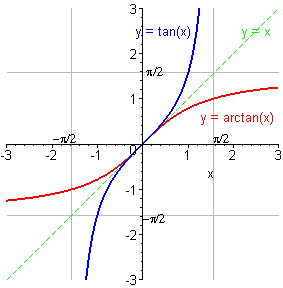
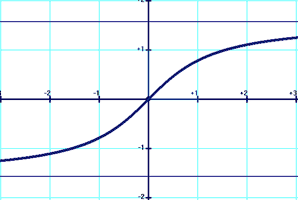
Fonctions trigonométriques hyperboliques Sinus hyperbolique [sh(x)] et argument sinus hyperbolique [ash(x)] 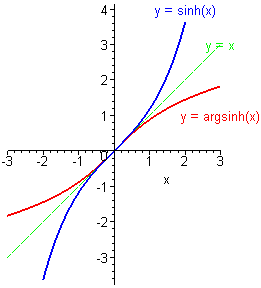 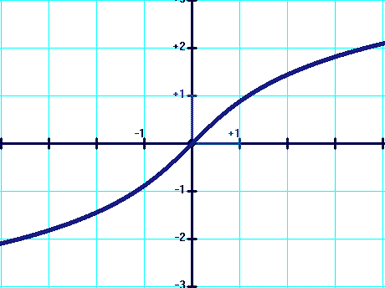
sh(x)=(ex-e-x)/2 ash(x)=ln[x+(1+x2)1/2] Cosinus hyperbolique [ch(x)] et argument cosinus hyperbolique [ach(x)]  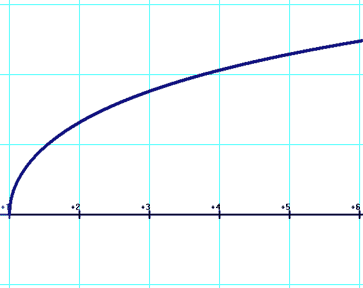
cosh(x)=(ex+e-x)/2 acosh(x)=ln[x+(x2-1)1/2] Tangente hyperbolique [th(x)] et argument tangente hyperbolique [ath(x)] 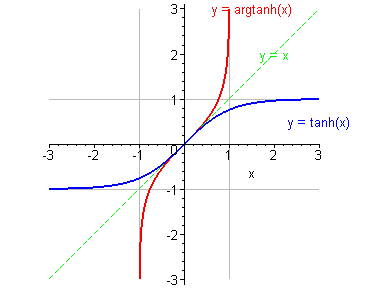 
th(x)=sh(x)/ch(x)=(ex-e-x)/(ex+e-x) ath(x)=1/2ln[(1+x)/(1-x)] Quleques fonctions trigonométriques Du style asin(x)/x, avec a une constante et x la variable. 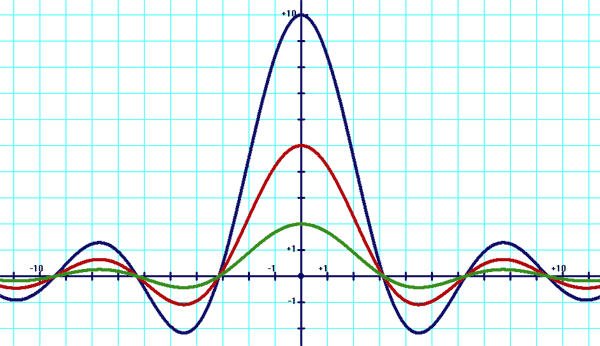
En bleu: y=10sin(x)/x En rouge: y=5sin(x)/x En vert: y=2sin(x)/x Du style sin(x)/ax, avec a une constante et x la variable. 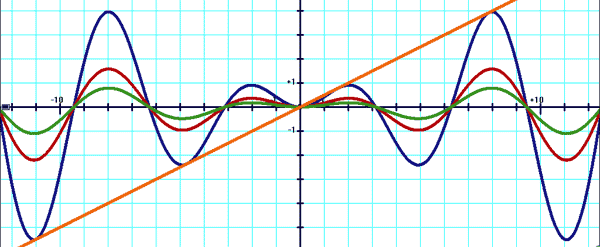
En bleu: y=sin(x)/2x En rouge: y=sin(x)/5x En vert: y=sin(x)/10x En orange:y=x/2 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonctions puissances Up Page Dans les fonctions puissances, du style xa, où a est une constante, on distingue quatre catégories de valeurs pour a: xn, x-n, x1/n, x-1/n, n étant un entier naturel positif. Puissances xn
Puissances x-n
Puissances x1/n
Puissances x-1/n

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonction valeur absolue Up Page Une fonction absolue, est une fonction qui ne prend jamais de valeurs négatives. Chaque portion de courbe qui se trouvait au préalable dans les "y" négatifs, se verra dessinait dans les "y" positifs, par le biais d'une symétrie horizontale.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonction partie entière Up Page La fonction "partie entière" consiste à récupérer seulement le nombre entier inférieur le plus proche de la valeur de y. La représentation graphique de ce type de fonction est une succession de marche d'escaliers.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les références Up Page Réseau Pepe Source Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonctions d'équation différentielle linéaire à coefficients constant du premier ordre Up Page Les systèmes du premier ordre sont toujours apériodiques. Charge et décharge La formule générale de ce type de fonction: y=a (1-e(-t/t)) pour la charge et y=a e(-t/t) pour la décharge. La valeur t (tau) étant la constante de charge (ou de décharge), e la fonction exponentielle et a la valeur maximale atteinte par la fonction lorsque la valeur t tend vers l'infini. Remarque importante: on ne s'intéressera qu'aux valeurs positives de t. La variable t a la même caractéristique que la variable x, toutefois dans le but de vous amener dans l'univers des fonctions remarquables, que j'aborderai plus tard (fonctions polaires et fonctions paramétriques), je vous invite à vous habituer à ce nouveau type de variable ! La constante t est significative, puisque elle vous informe sur le temps que prendra la fonction pour atteindre les 20%, 40% ... 80% de la valeur maximale. La valeur maximale ne sera jamais atteinte car il lui faudrait un temps infini à la fonction pour s'en approcher inexorablement. Deux valeurs sont à retenir: 1t et 5t. Au bout d'un t nous obtenons 63.2% de sa valeur max et 5t nous atteignons les 99.3%. Charge 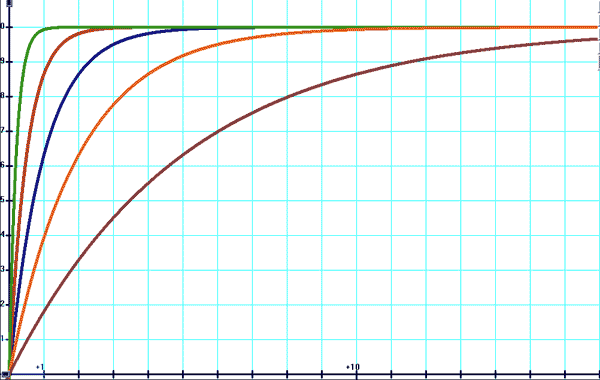
En bleu: y=10(1-e(-t)) En rouge: y=10(1-e(-2t)) En vert: y=10(1-e(-5t)) En orange: y=10(1-e(-t/2)) En marron: y=10(1-e(-t/5)) Décharge 
En bleu: y=10e(-t) En rouge: y=10e(-2t) En vert: y=10e(-5t) En orange: y=10e(-t/2) En marron: y=10e(-t/5) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Fonctions d'équation différentielle linéaire à coefficients constant du second ordre Up Page Discriminant nul 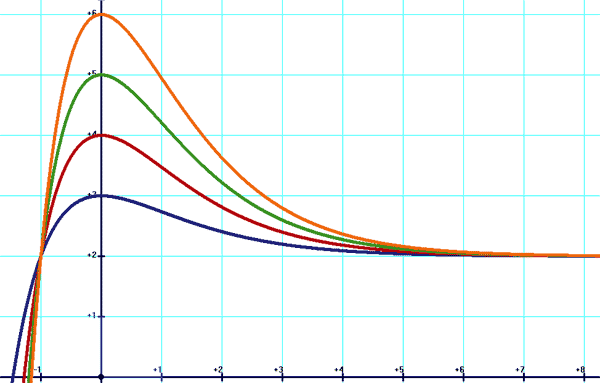
En bleu: y=(x+1)e(-x)+2 En rouge: y=2(x+1)e(-x)+2 En vert: y=3(x+1)e(-x)+2 En orange: y=4(x+1)e(-x)+2 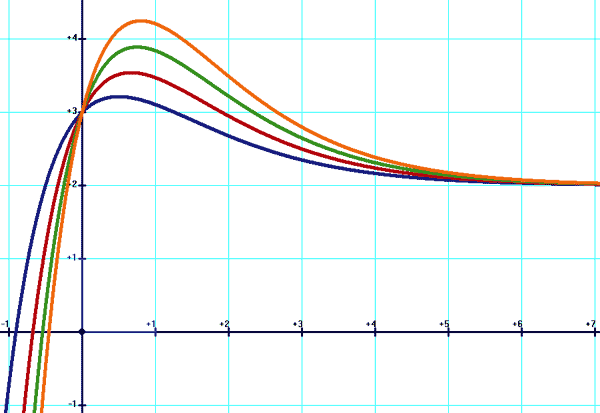
En bleu: y=(2x+1)e(-x)+2 En rouge: y=(3x+1)e(-x)+2 En vert: y=(4x+1)e(-x)+2 En orange: y=(5x+1)e(-x)+2 
En bleu: y=(x+1)e(-2x)+2 En rouge: y=(x+1)e(-3x)+2 En vert: y=(x+1)e(-7x/2)+2 En orange: y=(x+1)e(-x/2)+2 En marron: y=(x+1)e(-x/4)+2 Discriminant positif 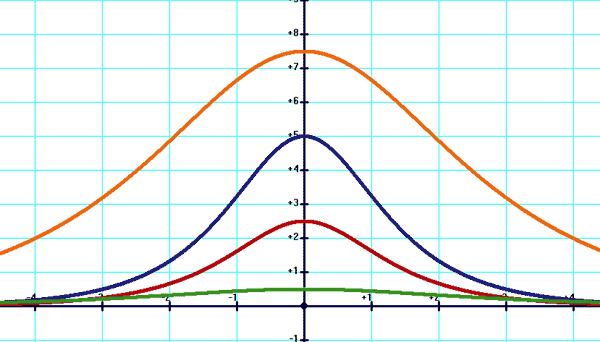
En bleu: y=10/(e(-x)+e(x)) En rouge: y=5/(e(-x)+e(x)) En vert: y=1/(e(-x)+e(x)) En orange: y=15/(e(-x)+e(x)) 
En bleu: y=10/(e(-x)+e(x)) En rouge: y=10/(e(-2x)+e(2x)) En vert: y=10/(e(-3x)+e(3x)) En orange: y=10/(e(-x/2)+e(x/2)) En marron: y=10/(e(-x/4)+e(x/4)) 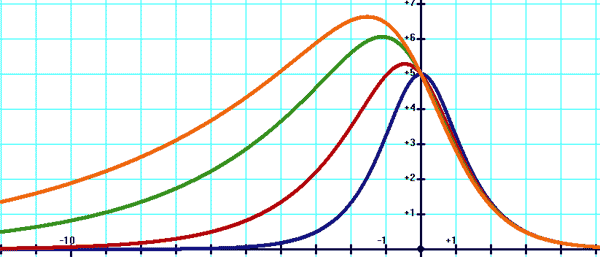
En bleu: y=10/(e(-x)+e(x)) En rouge: y=10/(e(-x/2)+e(x)) En vert: y=10/(e(-x/4)+e(x)) En orange: y=10/(e(-x/6)+e(x)) 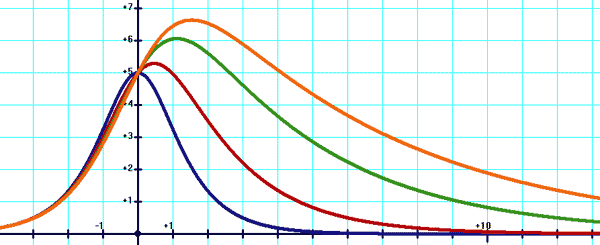
En bleu: y=10/(e(-x)+e(x)) En rouge: y=10/(e(-x)+e(x/2)) En vert: y=10/(e(-x)+e(x/4)) En orange: y=10/(e(-x)+e(x/6)) Discriminant négatif 
En bleu: y=10(e(-x/5) En rouge: y=-10(e(-x/5) En vert: y=-10(e(-x/5))cos(p+x)) En orange: y=-10(e(-x/5))sin(x) 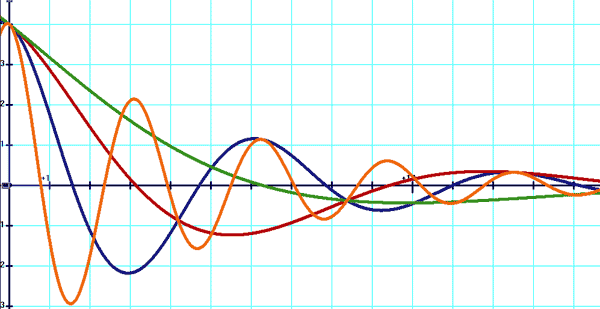
En bleu: y=-4(e(-x/5))cos(p+x)) En rouge: y=-4(e(-x/5))cos(p+x/2)) En vert: y=-4(e(-x/5))cos(p+x/4)) En orange: y=-4(e(-x/5))cos(p+2x)) 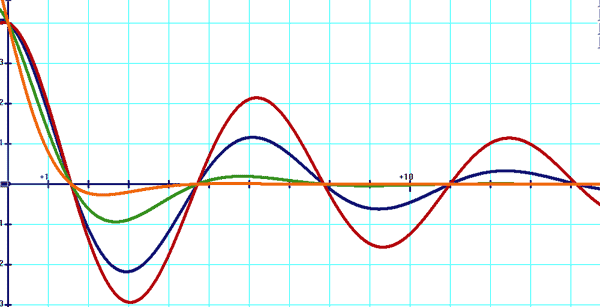
En bleu: y=-4(e(-x/5))cos(p+x)) En rouge: y=-4(e(-x/10))cos(p+x)) En vert: y=-4(e(-x/2))cos(p+x)) En orange: y=-4(e(-x))cos(p+x)) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Filtres de fréquence Up Page Fonctions de tranfert Du style a/[(1+(bx)2]1/2, avec (a,b) des constantes et x la variable. 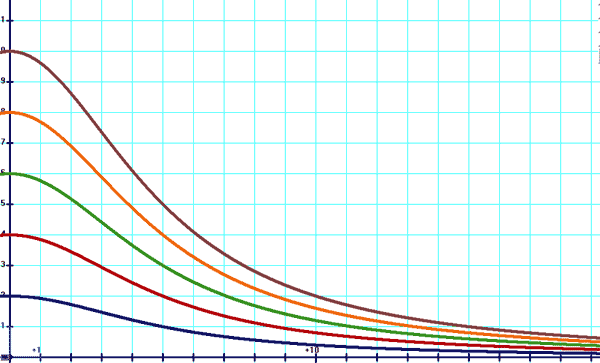
En bleu: y=2/[(1+(x/5)2]1/2 En rouge: y=4/[(1+(x/5)2]1/2 En vert: y=6/[(1+(x/5)2]1/2 En orange: y=8/[(1+(x/5)2]1/2 En marron: y=10/[(1+(x/5)2]1/2 Du style a/[(1-x2)2+4(bx)2]1/2, avec (a,b) des constantes et x la variable. 
En bleu: y=1/[(1-x2)2+4(x)2]1/2 En rouge: y=1/[(1-x2)2+4(2x)2]1/2 En vert: y=1/[(1-x2)2+4(8x/10)2]1/2 En orange: y=1/[(1-x2)2+4(5x/10)2]1/2 En marron: y=1/[(1-x2)2+4(3x/10)2]1/2

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Modulation Up Page Modulation d'amplitude Du style k[1+mcos(ax)]cos(bx), avec (k,m,a,b) des constantes et x la variable.
Modulation de fréquence Du style kcos[ax+msin(bx)], avec (k,m,a,b) des constantes et x la variable. 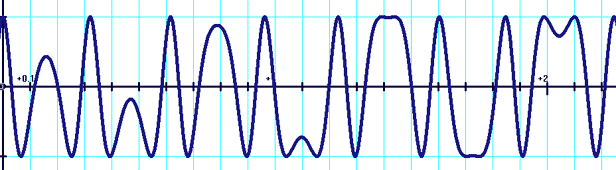
y=cos[x+5sin(10x)] 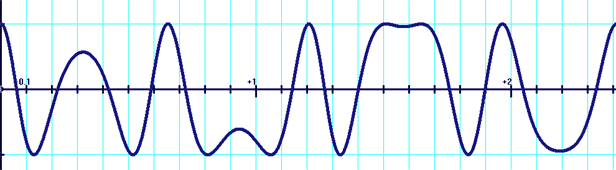
y=cos[x+5sin(5x)] 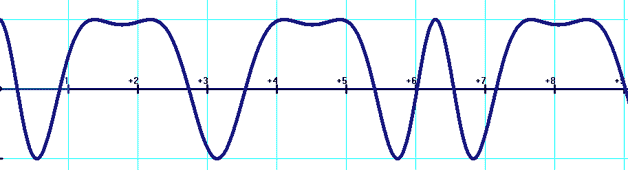
y=cos[x+5sin(x)] 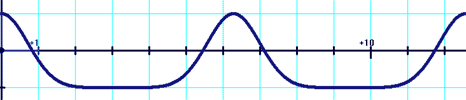
y=cos[x+sin(x)] 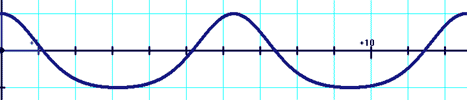
y=cos[x+(sin(x))/2] Du style ksin[ax+msin(bx)], avec (k,m,a,b) des constantes et x la variable. 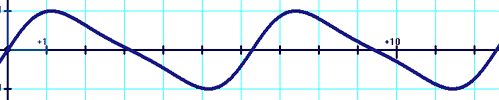
y=sin[x+(sin(x))/2] 
y=sin[x+sin(x)] 
y=sin[x+5sin(x)] 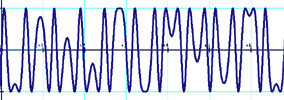
y=sin[x+5sin(5x)] 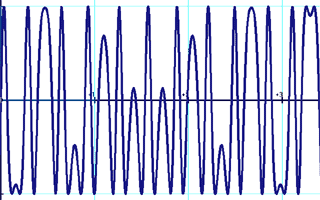
y=sin[x+5sin(10x)] Du style k1cos(ax)+k2cos(bx), avec (k1,k2,a,b) des constantes et x la variable.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mais encore ... Up Page 
|